重力電磁気学：Gravitoelectromagnetism

概要

　一般相対性理論で記述される重力場の方程式を，重力が弱い状況を考えて弱場近似の下で再定式化すると，驚くべきことに，電気磁気学の基礎方程式であるマクスウェル方程式と類似した方程式が導かれます．このように弱重力場を電磁気学との類推で議論することを重力電磁気学 (GEM: Gravitoelectromagnetism) といいます．ここでは，電磁気学のマクスウェル方程式に相当するGEM方程式を導いてみることにしましょう．

GEM方程式

弱場近似

　まず，弱重力場のもとでのアインシュタイン方程式の解を導くことにします．これにはちょうどレンス・ティリング解（ゆっくりと自転する天体がその外部に作り出す重力場）を使うことができます．これを再掲すると，
\begin{align}
ds^2 = -\left(1 + \dfrac{2\phi}{c^2} \right) c^2 dt^2 + \left( 1 -\dfrac{2\phi}{c^2} \right)\delta_{ij}dx^idx^j – \dfrac{4}{c} A_i dx^i dt \tag{1}
\end{align}
ここで，\(\phi, A_i, J^i \) はそれぞれ
\begin{align}
&\phi \equiv -\dfrac{GM}{r}, \tag{2} \\
&A_j \equiv \dfrac{G}{c} \dfrac{J^k x^\ell}{r^3} \varepsilon_{jk\ell}, \tag{3} \\
&J^j \equiv \int d^3x \ \rho\left( \boldsymbol{x} \right)\varepsilon^{j}_{\ k\ell} v^k x^\ell \tag{4}
\end{align}
と定義される量です．勘の良い人なら気づくかもしれませんが，\(\phi, A_i \) は電磁気学の電磁ポテンシャルに相当する物理量になっていて，\( \phi\) は重力電気ポテンシャル (gravitoelectric potential) ，\( \boldsymbol{A}\) は重力磁場ベクトルポテンシャル (gravitomagnetic vector potential) と呼ばれています．

ローレンツゲージ条件

　電磁場と同様にゲージ条件 \( \overline{h}^{\mu\alpha}_{\ \ \ ,\alpha}=0 \) から電磁ポテンシャルのローレンツゲージ条件に相当する恒等式を導いてみます. この弱場 \(h_{\mu\nu}\) はレンス・ティリング解の式(20)で具体形が示されています．これを使って，\(\mu=0\) 成分を実際に計算してみると，
\begin{align}
0&= \partial_0 h^{00} + \partial_j h^{0j} \\
&= \dfrac{1}{c} \dfrac{\partial\phi}{\partial t} + \dfrac{1}{2} \boldsymbol{\nabla}\cdot\boldsymbol{A} \tag{5}
\end{align}
となり，因子 \(\frac{1}{2}\) は別として，電磁ポテンシャルのローレンツゲージと一致することがわかります（ここの (8) 式と対応しています）．

重力電磁場

　そこで，電磁気学との類推から電場と磁場に相当する量を \(\phi, A_j\) から導いてみます．
\begin{align}
\boldsymbol{E}_G &= -\boldsymbol{\nabla}\phi – \dfrac{1}{2} \dfrac{\partial\boldsymbol{A}}{\partial c t}, \tag{6}\\
\boldsymbol{B}_G &= \boldsymbol{\nabla} \times \boldsymbol{A}\tag{7}
\end{align}
この \(\boldsymbol{E}_G, \boldsymbol{B}_G \) はそれぞれ重力電場(gravitoelectric field)と重力磁場(gravitomagnetic field)と呼ばれています（ここの (9) 式と (10) 式に対応しています）．

GEM方程式

　以上から，電磁気学のマクスウェル方程式に相当するGEM方程式が以下のように成り立つことがわかります：

\begin{align}
&\boldsymbol{\nabla} \cdot \boldsymbol{E}_G = -4\pi G\rho, \tag{8} \\
&\boldsymbol{\nabla} \cdot \boldsymbol{B}_G = 0, \tag{9} \\
&\boldsymbol{\nabla}\times\boldsymbol{E}_G = -\dfrac{1}{2c}\dfrac{\partial \boldsymbol{B}_G}{\partial t}, \tag{10} \\
&\boldsymbol{\nabla}\times\dfrac{1}{2}\boldsymbol{B}_G = -\dfrac{4\pi G}{c}\boldsymbol{j} + \dfrac{1}{c}\dfrac{\partial \boldsymbol{E}_G}{\partial t} \tag{11}
\end{align}
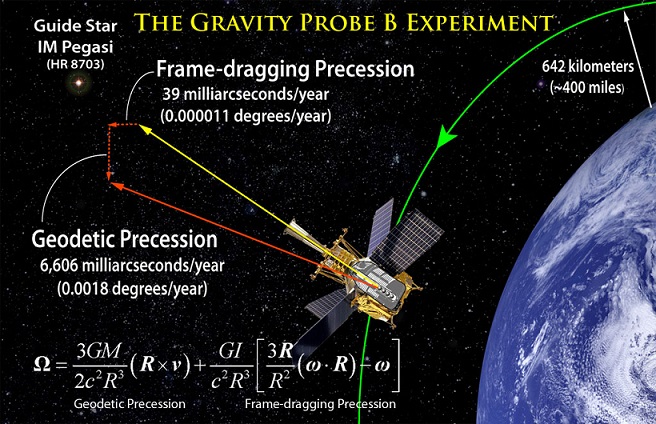
したがって，弱場近似のもとでは重力は電磁気学との類推で議論できることが示せました．このGEM方程式は，ゆっくり自転する天体の外部の重力場，例えば地球周囲の重力場にも適用可能です．そこで，近年ではGEM方程式から導かれる物理現象を，Gravity Probe Bという衛星実験で検証しようとする試みもあるようです。ちなみに，重力電磁場の詳細なレビューはGravitoelectromagnetism: A Brief Reviewにあるため，気になる人は読んでみてもいいかもしれないですね．