概要
この記事では,一般相対論を学ぶ上で最大の山場となる複雑なテンソルたちをMathematica の力を借りて計算してく方法を紹介します.ここではSchwarzschild解を例にとることにしましょう.最終的なゴールはアインシュタインテンソル \( G_{\mu\nu} \) を計算することです.そのために以下では,計量テンソル \(g_{\mu\nu}\) を設定し,クリストッフェル記号 \(\Gamma^{mu}{}_{\nu\rho}\) → リーマンテンソル \( R^{\mu}{}_{\nu\rho\sigma} \) → リッチテンソル \(R_{\mu\nu}\) → アインシュタインテンソル \( G_{\mu\nu} \) と順番に計算していくことにします.
Mathematicaでの計算
計量テンソル \(g_{\mu\nu}\)
まずはじめに,座標系を定義します.Schwarzschild計量では,真空で球対称な重力場を考えますので,極座標 \( x^{\mu} = \left(t, r, \theta, \phi \right) \) を座標系にとることにします.まだ,次元は時間+3次元空間なので合計で4です.Mathmatica で表すと,
dim = 4;
x := {t, r, \[Theta], \[Phi]}となります.次に計量 \(g_{\mu\nu} \) を定義していきましょう.球対称の重力場を考えているため,線素 \(ds^2\) は
\begin{align}
ds^2 = – e^{ 2\alpha\left(t,r\right)} c^2 dt^2 + e^{2\beta \left(t,r\right)} dr^2 + r^2 \left(d\theta^2 + \sin^2 \theta d^2 \phi \right) \tag{1}
\end{align}
と表すことができます.\(\alpha\left(t,r\right)\) と \(\beta\left(t,r\right)\) は \(t\) と \(r\) に依存する関数です.Mathematicaに計算はすべて任せるので,このまま進めても良いのですが,ここではわかりやすさのため \(t\) 依存性は落とすことにします(これはバーコフの定理で正当化できます.また,(1) 式は \(2\alpha\left(t,r\right)\) や \(2\beta\left(t,r\right)\) と2の因子がありますが,これは後々数式が簡単になるように見越して付けています).したがって,最終的に線素は
\begin{align}
ds^2 = – e^{ 2\alpha\left(r\right)} c^2 dt^2 + e^{2\beta \left(r\right)} dr^2 + r^2 \left(d\theta^2 + \sin^2 \theta d^2 \phi \right) \tag{2}
\end{align}
となります.これより,計量は下のように定義できます.
gdd = Table[0, {\[Mu], 1, dim}, {\[Nu], 1, dim}];
gdd[[1, 1]] = -c^2 * Exp[2*\[Alpha][r]];
gdd[[2, 2]] = Exp[2*\[Beta][r]];
gdd[[3, 3]] = r^2;
gdd[[4, 4]] = r^2*Sin[\[Theta]]^2;
guu = Inverse[gdd];\( \text{gdd} = g_{\mu\nu}, \text{guu} = g^{\mu\nu}\) と対応しています(d は下添字,u は上添字とします).gdd と guu の行列の具体的な要素をすべて表示すると下記の通りになります.MatrixForm で行列形式で表示できます.
gdd // Simplify // MatrixForm
guu // Simplify // MatrixForm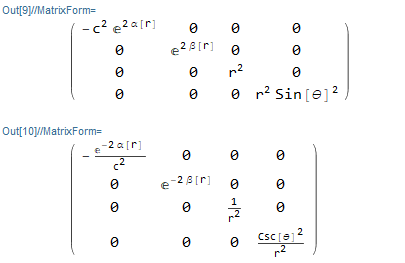
クリストッフェル記号 \(\Gamma^{\mu}{}_{\nu\lambda}\)
次のステップとして,クリストッフェル記号 \(\Gamma^{\mu}{}_{\nu\lambda}\) を計算します.これは定義より
\begin{align}
\Gamma^{\mu}{}_{\nu\lambda} = \dfrac{1}{2} g^{\mu\rho} \left( g_{\rho\nu, \lambda} + g_{\rho \lambda, \nu} – g_{\nu \lambda, \rho} \right) \tag{3}
\end{align}
と計量を使って計算ができます.(3) 式を Mathematica で表現すると次のようになります(Do でForループを回して各成分の計算をさせています).
Do[Christ[\[Mu], \[Nu], \[Lambda]] =
1/2*Sum[guu[[\[Mu], \[Rho]]]*(
D[gdd[[\[Rho], \[Nu]]], x[[\[Lambda]]]] +
D[gdd[[\[Rho], \[Lambda]]], x[[\[Nu]]]] -
D[gdd[[\[Nu], \[Lambda]]], x[[\[Rho]]]]),
{\[Rho], 1, dim}
], {\[Mu], 1, dim}, {\[Nu], 1, dim}, {\[Lambda], 1, dim}
];クリストッフェル記号の各成分を具体的に表現すると下記の通りになります.多くの成分は 0 となるため,ここでは 0 となる成分は表示をしないようにしていることに注意です(0 と等しくない成分を UnsameQ で指定しています).
ListChrist := Table[
If[UnsameQ[Christ[\[Mu], \[Nu], \[Lambda]], 0], {
Style[Subsuperscript[\[CapitalGamma], Row[{x[[\[Nu]]], x[[\[Lambda]]]}], x[[\[Mu]]]], 18],
"=",
Style[Christ[\[Mu], \[Nu], \[Lambda]] // FullSimplify, 14]}
], {\[Mu], 1, dim}, {\[Nu], 1, dim}, {\[Lambda], 1, \[Nu]}
];
TableForm[Partition[DeleteCases[Flatten[ListChrist], Null], 3], TableSpacing -> {1, 2}]
リッチテンソル \(R_{\mu\nu}\)
次に,リーマンテンソルとリッチテンソルを計算していきます.定義からリーマンテンソルとリッチテンソルは,計量とクリストッフェル記号を使って,
\begin{align}
&R^{\mu}{}_{\nu \rho \sigma}
= \Gamma^{\mu}{}_{\nu \sigma, \rho} – \Gamma^{\mu}{}_{\nu\rho,\sigma}
+ \Gamma^{\mu}{}_{\rho\lambda} \Gamma^{\lambda}{}_{\nu\sigma}
– \Gamma^{\mu}{}_{\sigma\lambda} \Gamma^{\lambda}{}_{\nu\rho}, \tag{4}\\
&R_{\mu\nu} = R^{\rho}{}_{\mu\rho\nu}, \tag{5}\\
&R = g^{\mu\nu} R_{\nu\mu} \tag{6}
\end{align}
と表すことができます.リーマンテンソルとリッチテンソルも計算も,先ほどと同様に Do 文を使ってMathematicaに各成分すべて計算させます.ここで,\(\text{Ruddd} = R^{\mu}{}_{\nu \rho \sigma}\),\( \text{Rdddd} = R_{\mu\nu\rho\sigma}\),\(\text{Rdd} = R_{\mu\nu}\) と表記しています.
Do[Ruddd[\[Mu], \[Nu], \[Rho], \[Sigma]] =
D[Christ[\[Mu], \[Nu], \[Sigma]], x[[\[Rho]]]] -
D[Christ[\[Mu], \[Nu], \[Rho]], x[[\[Sigma]]]] +
Sum[Christ[\[Mu], \[Rho], \[Lambda]]*
Christ[\[Lambda], \[Nu], \[Sigma]] -
Christ[\[Mu], \[Sigma], \[Lambda]]*
Christ[\[Lambda], \[Nu], \[Rho]],
{\[Lambda], 1, dim}
], {\[Mu], 1, dim}, {\[Nu], 1, dim}, {\[Rho], 1, dim}, {\[Sigma], 1, dim}
];
Do[Rdddd[\[Mu], \[Nu], \[Rho], \[Sigma]] =
Sum[
gdd[[\[Mu], \[Kappa]]] *
Ruddd[\[Kappa], \[Nu], \[Rho], \[Sigma]],
{\[Kappa], 1, dim}
], {\[Mu], 1, dim}, {\[Nu], 1, dim}, {\[Rho], 1, dim}, {\[Sigma], 1, dim}]
];
Do[Rdd[\[Mu], \[Nu]] =
Sum[Ruddd[\[Rho], \[Mu], \[Rho], \[Nu]], {\[Rho], 1, dim}],
{\[Mu], 1, dim}, {\[Nu], 1, dim}
];
R = Sum[Sum[guu[[\[Mu], \[Nu]]] Rdd[\[Nu], \[Mu]], {\[Mu], 1, dim}], {\[Nu], 1, dim}];先ほどと同じように 0 以外のリッチテンソルの具体的な成分を表示しましょう.
ListRdd := Table[
If[UnsameQ[Rdd[\[Mu], \[Nu]], 0],
{Style[Subscript[R, Row[{x[[\[Mu]]], x[[\[Nu]]]}]], 18],
"=",
Style[Rdd[\[Mu], \[Nu]] // FullSimplify, 16]}
], {\[Nu], 1, 4}, {\[Mu], 1, \[Nu]}
];
TableForm[Partition[DeleteCases[Flatten[ListRdd], Null], 3], TableSpacing -> {1, 2}]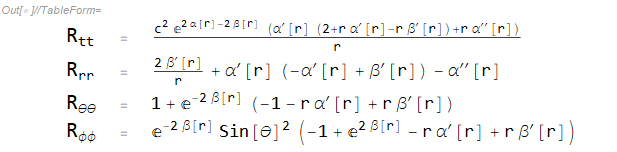
R // FullSimplify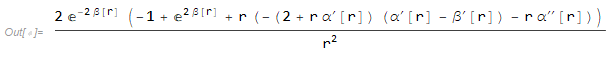
アインシュタインテンソル \(G_{\mu\nu}\)
次に,アインシュタインテンソルを計算していきます.
\begin{align}
&G_{\mu\nu} = R_{\mu\nu} – \dfrac{1}{2} g_{\mu\nu} R, \tag{7} \\
&G^{\mu}{}_{\nu} = g^{\mu\kappa}R_{\kappa \nu} \tag{8}
\end{align}
これを Mathematica で表現すると,やはり先ほどと同じで Do 文を使って下記の通り計算できます.
Do[Gdd[\[Mu], \[Nu]] =
Rdd[\[Mu], \[Nu]] - 1/2*gdd[[\[Mu], \[Nu]]]*R, {\[Mu], 1, dim}, {\[Nu], 1, dim}
];
Do[Gud[\[Mu], \[Nu]] =
Sum[
guu[[\[Mu], \[Kappa]]]*Gdd[\[Kappa], \[Nu]],
{\[Kappa], 1, dim}
], {\[Mu], 1, dim}, {\[Nu], 1, dim}
];0 以外の具体的な成分も同様に下記の通り表示できます.これでテンソル計算は終わりです.
ListGdd := Table[
If[UnsameQ[Gdd[\[Mu], \[Nu]], 0],
{Style[Subscript[G, Row[{x[[\[Mu]]], x[[\[Nu]]]}]], 18],
"=",
Style[Gdd[\[Mu], \[Nu]] // FullSimplify, 16]}
], {\[Nu], 1, 4}, {\[Mu], 1, \[Nu]}
];
ListGud := Table[
If[UnsameQ[Gud[\[Mu], \[Nu]], 0],
{Style[Subsuperscript[G, Row[{x[[\[Nu]]]}], x[[\[Mu]]]], 18],
"=",
Style[Gud[\[Mu], \[Nu]] // FullSimplify, 16]}
], {\[Nu], 1, 4}, {\[Mu], 1, \[Nu]}
];
TableForm[Partition[DeleteCases[Flatten[ListGdd], Null], 3], TableSpacing -> {1, 2}]
TableForm[Partition[DeleteCases[Flatten[ListGud], Null], 3], TableSpacing -> {1, 2}]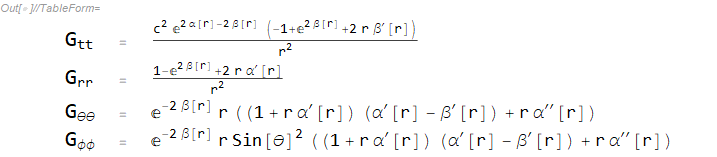
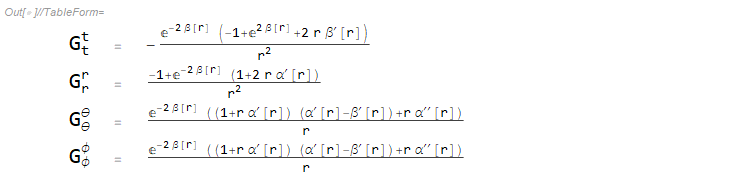
アインシュタイン方程式
最後にアインシュタイン方程式を解いていきましょう.アインシュタイン方程式は,今は球対称で真空の重力場を考えているので,エネルギー運動量テンソルは原点以外では 0 なので,
\begin{align}
G^{\mu}{}_{\nu} = 0 \tag{9}
\end{align}
となります.\(G^{\mu}{}_{\nu} \) の具体的な成分を見ると,\( G^{t}{}_t\) 成分は \(\beta\) のみで表されているので,まずはこの微分方程式を解くことにします.ここまでくると,手計算でも簡単ですが,せっかくなので Mathematica に最後までやらせることにしましょう.無限遠では計量はミンコフスキー計量と一致するので,境界条件は \( \beta \left(\infty \right) = 0\) となります.したがって,下記のように解けます.
(sol = DSolve[
{Gud[1, 1] == 0, \[Beta][Infinity] == 0},
\[Beta][r], r]
) // Quiet // Simplify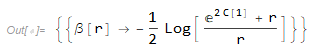
これで \(\beta\) が求まったので,\( G^{r}{}_{r} \) に代入をして,\(\alpha\) についての微分方程式を解いていきます.これも同様に,無限遠では計量はミンコフスキー計量と一致するので,境界条件は \( \alpha \left(\infty \right) = 0\) となります.したがって,下記のように解けます.
DSolve[
{Gud[2, 2] == 0 /. sol[[1]], \[Alpha][Infinity] == 0},
\[Alpha][r], r
] // Quiet // Simplify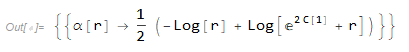
あとはこの積分定数 \(C_1\) を決めるだけです.上式は整理すると,
\begin{align}
&e^{2\alpha \left(r\right)} = 1 + \dfrac{e^{2C_1}}{r}, \tag{10} \\
&e^{-2\beta \left(r\right)} = 1 + \dfrac{e^{2C_1}}{r} \tag{11}
\end{align}
となります.中心に質点 \(M\) があるとしてニュートン極限を考えると,\( g_{tt} \cong -\left(1 – \frac{2GM}{c^2r}\right) \) となるので,結局, \(e^{2\alpha \left(r\right)} = e^{-2\beta \left(r\right)} = 1 – \frac{2GM}{c^2r} \) と求まります.以上より,Schwarzschild計量を
\begin{align}
ds^2 = – \left( 1 – \dfrac{2GM}{c^2r}\right) c^2 dt^2 + \dfrac{1}{ 1 – \frac{2GM}{c^2r}} dr^2 + r^2 \left(d\theta^2 + \sin^2 \theta d^2 \phi \right) \tag{12}
\end{align}
と求めることができました.
以上からわかるように,一度ベースとなるコードさえ書いてしまえば,後は計量 \(g_{\mu\nu} \) の具体的な数式を変更するだけです.ここでは,Schwarzschild計量を例にとってアインシュタインテンソルまで計算しましたが,他の計量(FLRW計量やReissner‐Nordstrøm計量とか)でもまったく同じように,具体的な計量の形を指定さえすれば,あとはエンターキーを押すだけで,複雑なテンソル計算ができてしまいます.
ただし,重力波やブラックホール摂動論のような摂動計算は若干コツが必要なので,それは別の記事で紹介することにしましょう. また,このままではテンソルのまま抽象的に計算することはできません.そのためには,xTensorのようなパッケージが必要になることに注意が必要です.Mathematica は有料ソフトなので人によっては, Maxima のような無償数式処理ソフトを愛用している人もいるかもしれません.こちらでも簡単にテンソル計算ができるので,時間があれば紹介したいと思います.


コメント